偏心状态下的轴向磁通永磁电机受力分析
【作者】:网站采编
【关键词】:
【摘要】偏心状态下的轴向磁通永磁电机受力分析 张霄霆 1 张炳义 1 曹永鹏 2 (1. 沈阳工业大学电气工程学院 沈阳 110870 2. 重庆金康动力新能源有限公司 重庆 400032) 摘要 为了研究偏心对轴向
偏心状态下的轴向磁通永磁电机受力分析
摘要 为了研究偏心对轴向磁通永磁电机受力影响,该文建立了理想状态下轴向磁通永磁电机的气隙磁场解析计算模型,并通过引入气隙磁导函数计及了开槽对气隙磁场的影响;通过对轴向磁通永磁电机偏心状态的分析,建立了偏心状态下气隙磁场解析计算模型,并通过有限元法验证了解析计算模型的准确性。在此基础上,构建了偏心状态下轴向磁通永磁电机不平衡磁拉力受力计算模型,对不平衡磁拉力进行了计算分析。无论是静态偏心还是动态偏心,随着偏心率的增加,不平衡磁拉力幅值逐渐增加。静态偏心下,不平衡磁拉力不随时间发生变化;动态偏心下,不平衡磁拉力呈周期性变化。
关键词:轴向磁通永磁电机 气隙磁通密度 偏心 不平衡磁拉力
0 引言
轴向磁通永磁电机具有转矩密度高、轴向尺寸小、结构紧凑的优点,在飞轮储能、风力发电、电动汽车等领域具有广阔的应用前景[1-2]。由于轴向磁通永磁电机结构的特殊性,在其设计过程中,为了得到准确的性能参数,往往需要构建三维有限元计算模型,耗时耗力。同时,由于制造装配过程中的误差以及电机运行过程中所受的冲击力的影响,轴向磁通永磁电机定子与转子轴线易发生偏移,导致转子偏心。转子偏心对电机损耗、受力、振动噪声等性能有显著影响[3-4],因此有必要研究轴向磁通永磁电机偏心状态下的性能。
随着对电机性能要求的提高,偏心情况下电机受力与振动得到了越来越多的研究。文献[5]建立了转子偏心磁通密度计算方程,并引入扰动理论对偏心下的气隙磁场进行计算,并将解析计算结果与有限元计算结果进行比较,二者计算结果基本一致,但该方法在实际计算中较为复杂。文献[6]引入傅里叶级数展开的方法对静态偏心下的气隙磁通密度进行计算分析,该方法计算精度高,易编程,但未考虑端部效应的影响。文献[7]分析了集中绕组永磁电机偏心状态下的电磁力,基于傅里叶变换得到了偏心引起的力波阶次,为电机偏心状态的监测提供了参考。文献[8]采用有限元法(Finite Element Method, FEM)分析了倾斜偏心对电机电磁力的影响,但有限元计算耗时。文献[9-10]通过对轴向磁通永磁电机进行分环处理,逐环计算求得电机气隙磁通密度的分布,最后通过对气隙磁通密度的叠加得到整个电机的气隙磁通密度分布。该方法计算简单,但随着分环数的增加,计算繁琐度增加。文献[11]采用有限元法分析了静态偏心对轴向磁通永磁电机气隙磁通密度与反电动势的影响,三维有限元法虽然能够准确计算轴向磁通永磁电机偏心状态下的磁通密度分布,但三维有限元法计算耗时耗力,不利于对偏心状态下电机性能进行快速计算与分析。文献[12]研究了静态偏心下的永磁电机磁通密度计算方法,采用等效剩磁法对偏心状态下的磁通密度进行计算,通过剩磁的不均匀程度来等效气隙的不均匀度。
通过以上分析可知,目前对轴向磁通永磁电机偏心状态下的研究相对较少,多采用有限元法,较为耗时,因此,有必要研究轴向磁通永磁电机偏心状态下的解析计算方法,在保证计算精度的前提下提高计算速度。
本文以一台额定功率10kW、额定转速1 500r/min的轴向磁通永磁电机为例,建立了理想状态下的气隙磁场解析计算模型,为了在计算中计及开槽与端部效应的影响,引入开槽气隙磁导函数与端部效应函数,然后,分析了偏心状态下的气隙长度变化,对偏心状态下的气隙磁导进行傅里叶分解,形成傅里叶函数,建立偏心状态下的气隙磁场解析计算模型,最后基于偏心状态下的解析计算模型分析了偏心对不平衡磁拉力的影响。
1 电机模型与结构
本文所研究的轴向磁通永磁电机为双定子单转子结构,永磁体为扇形,定子采用分数槽集中绕组,电机三维模型如图1所示。轴向磁通永磁电机参数见表1。
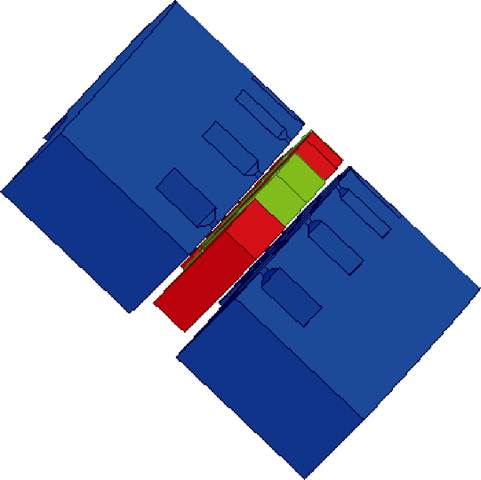
图1 轴向磁通永磁电机三维模型
Fig.1 3D model of axial flux permanent magnet machine
表1 轴向磁通永磁电机参数
Tab.1 Parameters of axial flux permanent magnet machine

参 数数 值 额定功率/kW10 极对数10 气隙长度/mm1 永磁体剩磁/T1.23 额定转速/(r/min)1 500 槽数24 极弧系数0.83 电机结构双定子单转子
2 气隙磁场解析计算模型
2.1 无偏心状态下的气隙磁场
为了方便推导气隙磁场的解析表达式,在推导过程中对轴向磁通永磁电机作如下简化:
(1)忽略定子铁心的饱和效应,不计定子铁心磁阻。
(2)永磁体退磁曲线为直线。
对于轴向磁通永磁电机,在考虑定子开槽、端部效应影响下,空载气隙磁通密度的表达式为
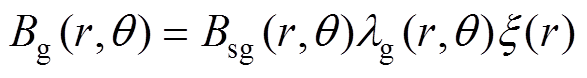 (1)
(1)
式中,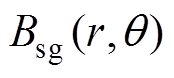 为未考虑齿槽效应、端部效应时的气隙磁通密度;
为未考虑齿槽效应、端部效应时的气隙磁通密度;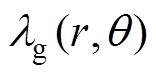 为开槽引起的气隙磁导函数;
为开槽引起的气隙磁导函数;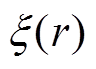 为端部效应函数。
为端部效应函数。
首先分析定子表面光滑情况下,即定子铁心无槽时气隙磁通密度的分布情况。无槽情况下,轴向磁通永磁电机的物理模型如图2所示。
部分指标判识原则:指由下一级预警结果确定高级别预警结果过程中,指标获取不全时按照已经获取指标判断的最高级别等级向上一级预警结果传递,待其他指标获取时重新按照最高级别原则重新上传。
财税激励政策为企业技术创新提供了有力支持,但由于激励政策的不完善,企业自身认识不足,影响了财税激励政策激励效用的发挥。
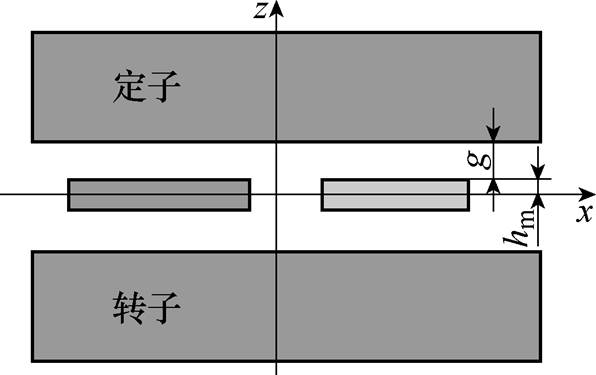
图2 无槽时的物理模型
Fig.2 Slotless physical model
基于图2所示的模型,得到永磁体剩余磁场强度分布如图3所示,由图3可知,两极间的剩余磁场强度为零。
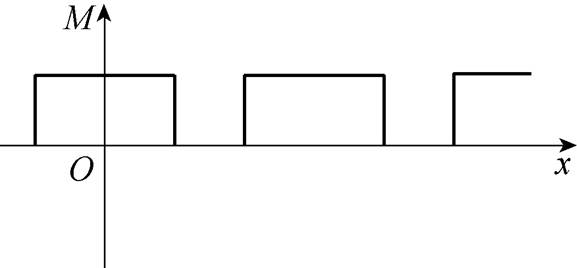
图3 永磁体剩余磁场强度分布
Fig.3 Magnetization distribution produced by PM
将图3所示的剩余磁场强度进行傅里叶分解可得
未偏心状态下,轴向磁通永磁电机定子与转子的轴向受力均匀;转子发生偏心后,定子与转子轴向受力不均匀,产生不平衡磁拉力,在小气隙处轴向力幅值增加,大气隙处轴向力幅值减小。轴线磁通永磁电机轴向力波为
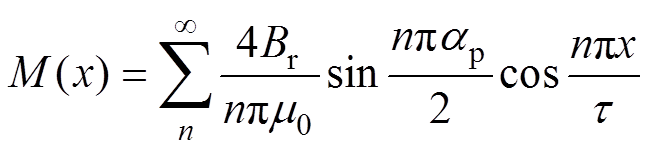 (2)
(2)
式中,Br为永磁体剩余磁通密度;ap为极弧系数;t 为极距;m0为真空磁导率。
通过求解剩余磁场强度的旋度,得到电流密度JM表达式为
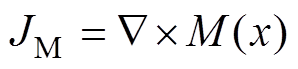 (3)
(3)
基于图2所示的物理模型,气隙区域与永磁体区域处的磁矢位满足拉普拉斯方程与泊松方程,有
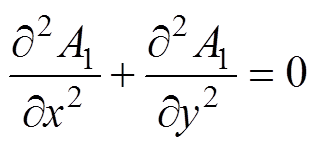 (4)
(4)
 (5)
(5)
在求得磁矢位的基础上,求其旋度,得到磁通密度的表达式为
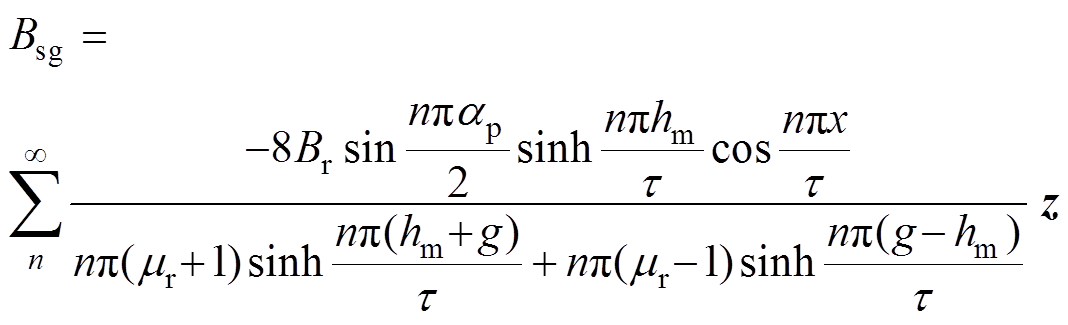 (6)
(6)
式中,g为气隙长度;hm为永磁体厚度。
为了计算方便,基于轴向磁通永磁电机的结构特点,将式(6)转换到柱坐标系下,有
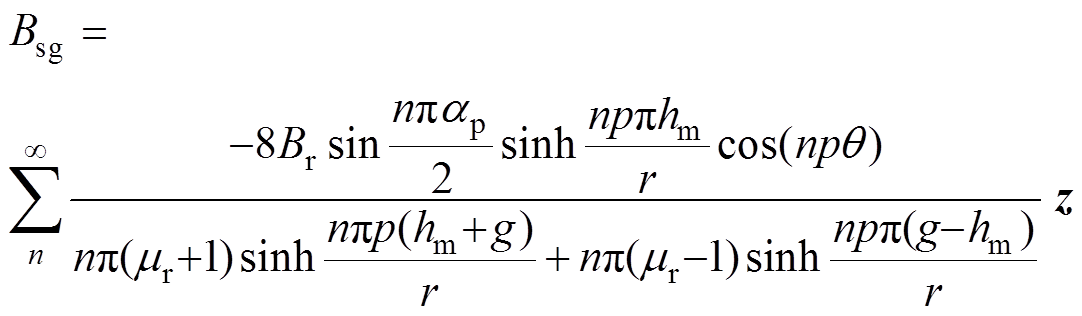 (7)
(7)
考虑端部效应后,解析计算得到的气隙磁通密度与有限元法得到的气隙磁通密度如图6所示。
2.2 开槽后的气隙磁场
定子开槽后,开槽区域的磁阻增大,磁场走向发生变化,开槽处的气隙磁通密度减小,由于齿谐波的影响,开槽后的气隙磁通密度谐波含量增加。为了计算开槽后的轴向磁通永磁电机气隙磁通密度,引入气隙磁导函数,有
综上所述,健康教育在高血脂患者中有着重要的应用价值,有效的将血脂控制在正常范围内,提高患者自我管理能力。
hm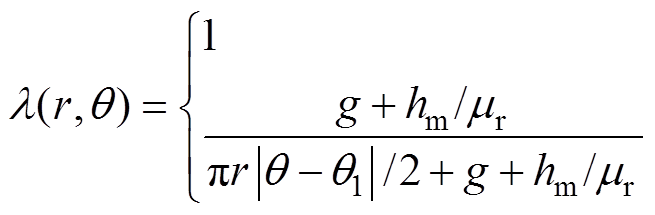 (8)
(8)
式中,q1为定子齿边距齿中心的距离。
对气隙磁导函数展开傅里叶分解,有
为了接受社会监督,防止不法人员冒充评估师从事评估业务,便于委托人和社会公众等查询某一评估专业人员是否通过了评估师资格考试,本法对评估行业协会公布评估师名单作了规定。
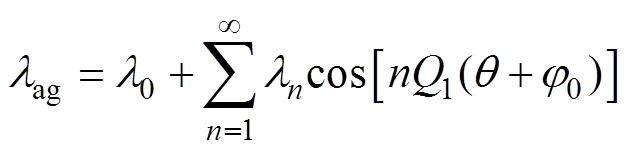 (9)
(9)
式中,Q1为定子槽数;l0为气隙磁导直流分量;j0为初始相位;ln为气隙磁导谐波分量。
基于式(9)计算得到的气隙磁导波形如图4所示。
根据回归结果显示,主要解释变量GDP增长率对碳排放量的影响呈现正向,解释了67%的部分,且在1%的显著水平上显著,说明湖北省在近20年的时间里,经济增长在很大程度上影响了碳排放。虽然代表经济发展和产业结构的第二产业占比也对其显示正向影响,但结果并不显著,人口规模和对外贸易规模也是同样的情况,说明除了经济增长,在武汉这样的非暖气供应的内陆城市,其他因素对于碳排放的影响程度较小。
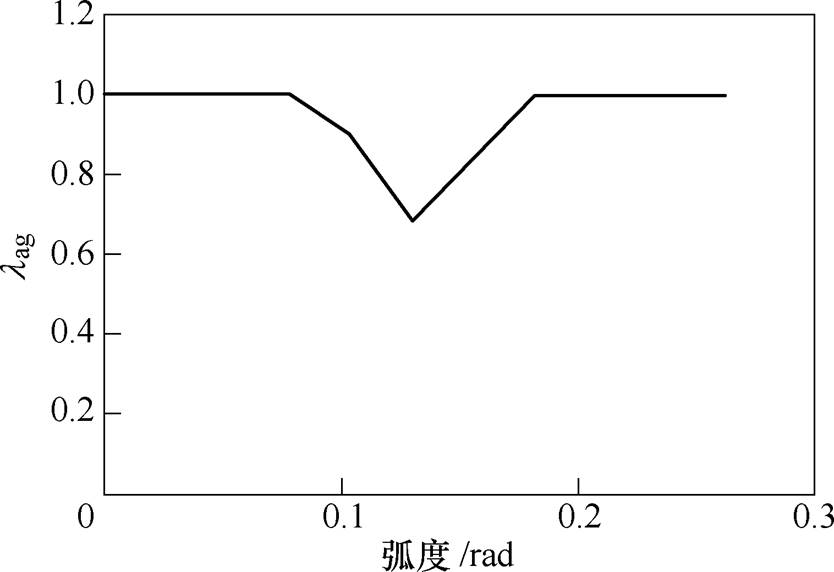
图4 气隙磁导波形
Fig.4 Permeance waveform of air gap
2.3 端部效应影响
基于有限元法得到的轴向磁通永磁电机磁极中心线处的气隙磁通密度波形如图5所示。从图中可以看出,磁通密度在端部处较小,表现出端部效应,因此轴向磁通永磁电机的端部效应不可忽略。
由POD分解可知,圆柱尾流中包含复杂的流动,既有大尺度的卡门涡街结构,又有大量的小涡和散涡。为更加清晰地识别流场中的主导结构,基于POD数据后处理软件对流场进行重构,重构结果见图7。

图5 基于有限元法计算得到的气隙磁通密度波形
Fig.5 Air gap flux density with FEM
为了在解析计算中考虑端部效应对气隙磁通密度的影响,本文引入端部效应修正函数,有
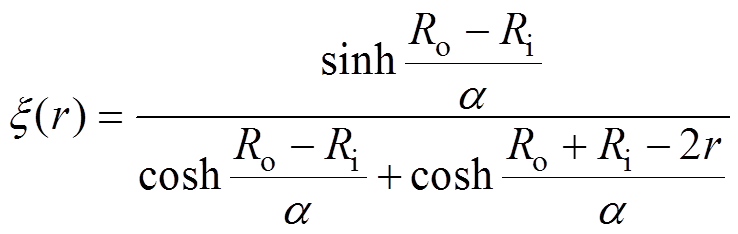 (10)
(10)
式中,a 为转子偏心方向的角度;Ro为转子外径;Ri为转子内径。
式中,mr为永磁体相对磁导率;p为极对数。
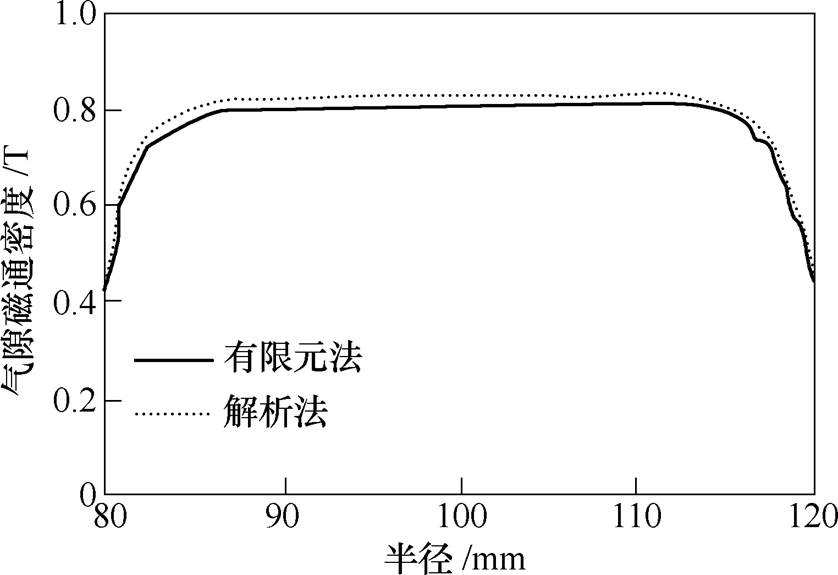
图6 解析法与有限元法磁通密度对比
Fig.6 Comparison of flux density between analytical method and FEM
3 轴向磁通永磁电机偏心状态分析
3.1 偏心状态下的磁通密度分布
轴向磁通永磁电机偏心状态分为静态偏心、动态偏心与混合偏心。轴向磁通永磁电机静态偏心情况下,定子与转子的几何中心不重合,但电机转子仍然绕转子轴线旋转;动态偏心情况下,电机定子与转子几何中心不重合,转子绕着定子轴线旋转;混合偏心包含静态偏心与动态偏心。
动态偏心状态下,解析法与有限元法计算得到的气隙磁通密度如图9所示,解析计算结果与有限元法计算所得结果基本一致,证明了解析计算方法的准确性。
官僚主义在领导上体现为老爷主义,即妄自尊大,爱耍官威;在工作上则表现为敷衍塞责的形式主义。而应对形式主义的,往往是心照不宣的官僚主义。可以说,官僚主义“逼出”了形式主义,形式主义迎合了官僚主义,二者如影相随,不分你我。
轴向磁通永磁电机偏心方向角度示意图如图7所示。其中,Os为电机定子几何中心,Or为转子几何中心。
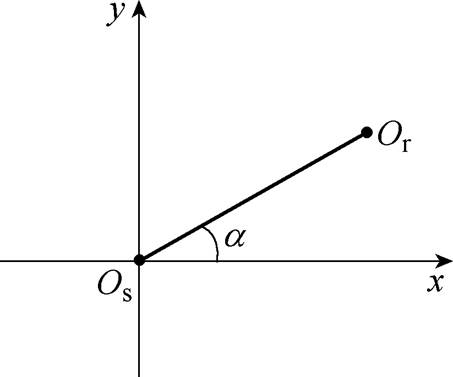
图7 偏心方向角度示意图
Fig.7 Schematic representation of eccentricity
根据轴向磁通永磁电机静态偏心原理,静态偏心下,气隙长度与转子的旋转无关。静态偏心下的气隙长度与转子位置角q 和偏心角度a 相关,静态偏心下的气隙长度为
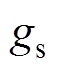
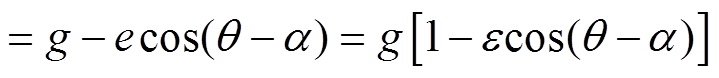 (11)
(11)
式中,e为定转子间最大偏心距;e =e/g为偏心率。
在求得偏心气隙长度的基础上,求得静态偏心时的气隙磁导为
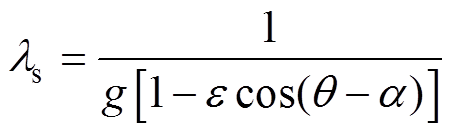 (12)
(12)
对其进行傅里叶展开,可得
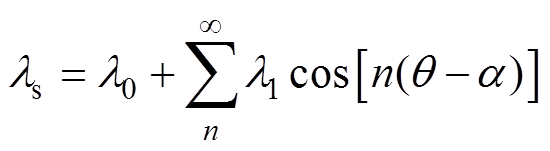 (13)
(13)
静态偏心状态下,解析法与有限元法计算得到的气隙磁通密度波形如图8所示,解析计算结果与有限元法计算所得结果基本一致,证明了解析计算方法的准确性。
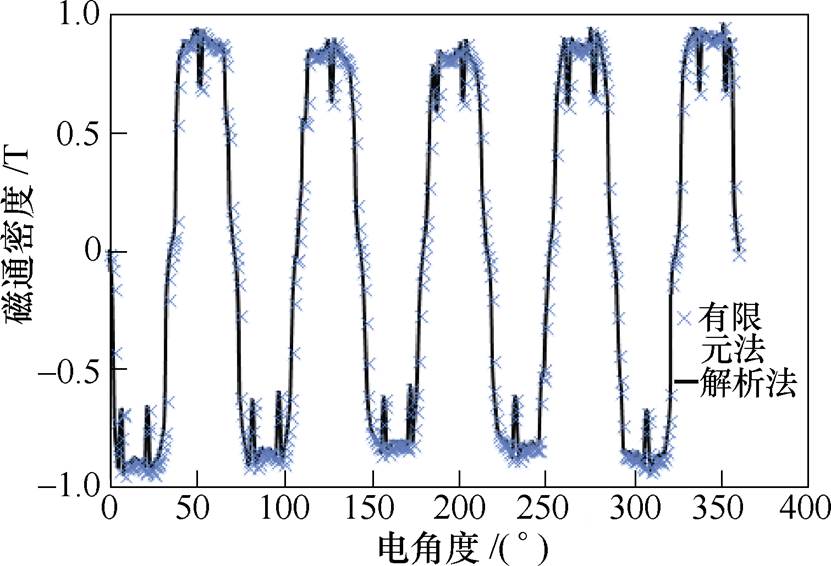
图8 静态偏心下解析法与有限元法计算结果对比
Fig.8 Comparison of air gap flux density between analytical method and FEM with static eccentricity
动态偏心情况下,转子绕定子轴线旋转,电机气隙长度与转子旋转周期有关,动态偏心状态下的气隙长度不仅与转子位置角、初始偏心角有关,还与旋转时间相关。动态偏心下,电机气隙长度为
苗床设置在温棚中。温棚东西走向,长30 m,宽12 m,高2.7 m,钢筋骨架,覆盖材质为长寿无滴膜,夏季有黑色遮荫网覆盖。
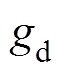
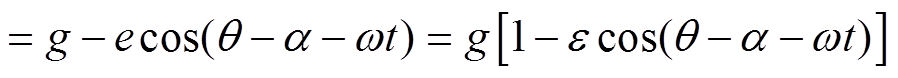 (14)
(14)
动态偏心下,求得气隙磁导为
管理工作的根本都要有人去操作,因此,提高管理层及从业人员的成本管控意识是解决企业成本管控问题的思想基础。首先,要加强管理层的成本管控意识。多进行相关管理意识的培训,多参观同行或先进企业,从上层加强成本管控意识。其次,加强从业人员的管控意识。在工作中不断的渗透成本管控理念,让各部门从业人员意识到成本管控不仅仅只是某一个部门的工作,而是涉及到企业各个职能部门的配合。使得各个部门的员工都参与到企业成本管控工作中。在不断调动从业人员积极性的同时,选取中层领导及有积极潜能的员工,有针对性的进行培训,从而提高他们的成本管控的专业技能。
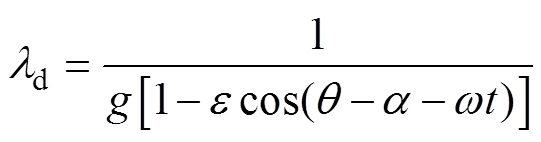 (15)
(15)
对式(15)进行傅里叶分解可得
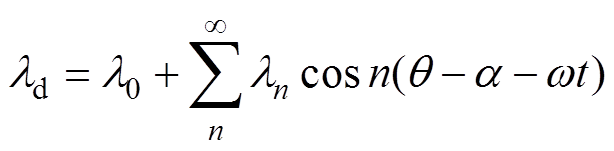 (16)
(16)
偏心导致轴向磁通永磁电机气隙长度不均匀,不均匀的气隙长度导致电机定转子之间的气隙磁导、磁通密度等参数发生变化,导致电机不平衡磁拉力增加,电机受力不均,恶化电机的振动与噪声。
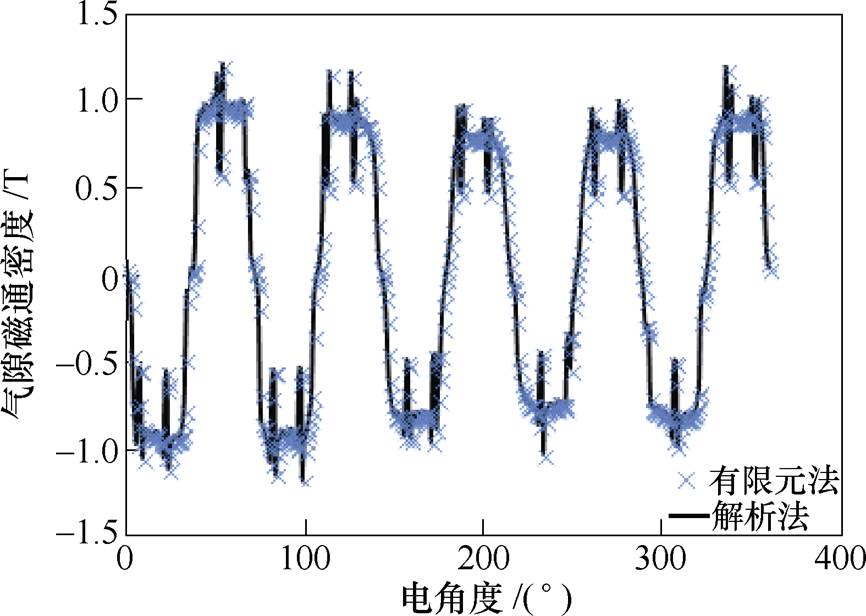
图9 动态偏心下气隙磁通密度解析法与有限元法对比
Fig.9 Comparison of air gap density between analytical method and FEM with dynamic eccentricity
3.2 偏心状态下的受力分析
作者简介: 何聪亮,男,汉族,福建省云霄县第一实验小学,云霄县优秀教师,一级教师,专科学历,研究方向:不断激发小学生学习数学的兴趣。
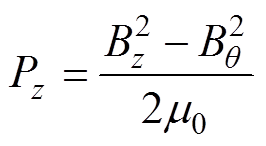 (17)
(17)
式中,Bz为轴向磁通密度;Bq 为切向磁通密度。
4.特定项目的特定风险。PPP项目的适用范围较广,每类项目均有其特定的风险。比如公路类项目的交通流量预测不准、收费标准的调整、项目成本增加、出现竞争线路等各类风险;轨道交通项目涉及不同地区和部门的合作风险、收费标准风险等;供水、电、气项目存在价格受限、非法偷用风险、施工风险等。
转子中微元体所受的电磁力为
在信息化日渐加深的今天,课题上直接传授知识的“满堂灌”已经不能起到很好的效果,学员们思维活跃,并且注意力更难以长时间的集中,需要使用学员关心的案例来激发他们的学习兴趣,提高学员课堂参与度,来达到更好的教学效果。
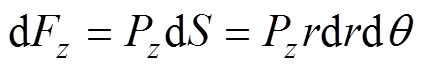 (18)
(18)
对应力进行积分分解,求得x、y方向的不平衡磁拉力分别为
在全球经济一体化的背景下,国际财经合作是一种必然。但是,随着金融危机以及近年来美国经济政策的不稳定,国际财经合作出现了较为明显的波动,影响了系统的整体稳定性。为此,本文以新时期为基本背景,探究国际财经合作的具体特征以及对于我国经济发展的影响与作用。并从国际变化、新形势冲击以及国内消费市场等三个维度对后续我国参与国际财经合作体系治理提出了相关的建议,希望能够为后续的平稳发展提供必要基础。
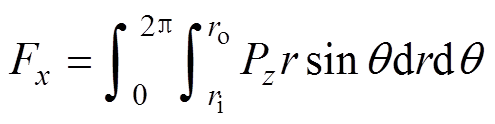 (19)
(19)
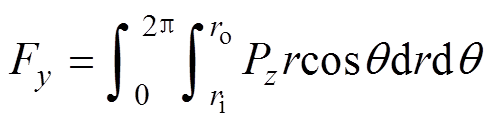 (20)
(20)
静态偏心下计算得到的不平衡磁拉力如图10所示。由于只在x方向发生静态偏心,因此只有x方向存在不平衡磁拉力,随着偏心率的增大,不平衡磁拉力逐渐增加,且不平衡磁拉力不随时间变化。
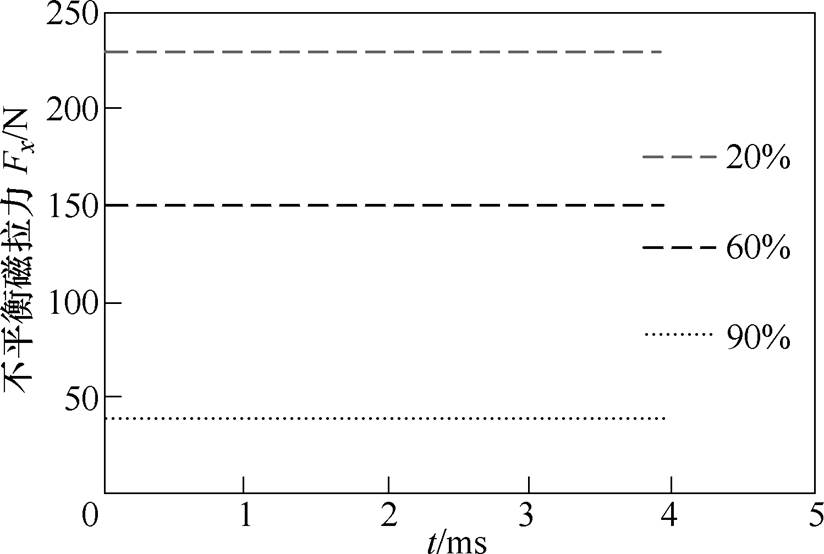
图10 静态偏心下x方向的不平衡磁拉力
Fig.10 Unbalanced magnetic force under static eccentricity of x direction
动态偏心下,偏心率对不平衡磁拉力Fx与Fy的影响如图11和图12所示。与静态偏心不同,动态偏心下,电机在x方向与y方向均产生不平衡磁拉力,且不平衡磁拉力随时间变化产生周期性波动,随着偏心率的增大,不平衡磁拉力的幅值逐渐增加。
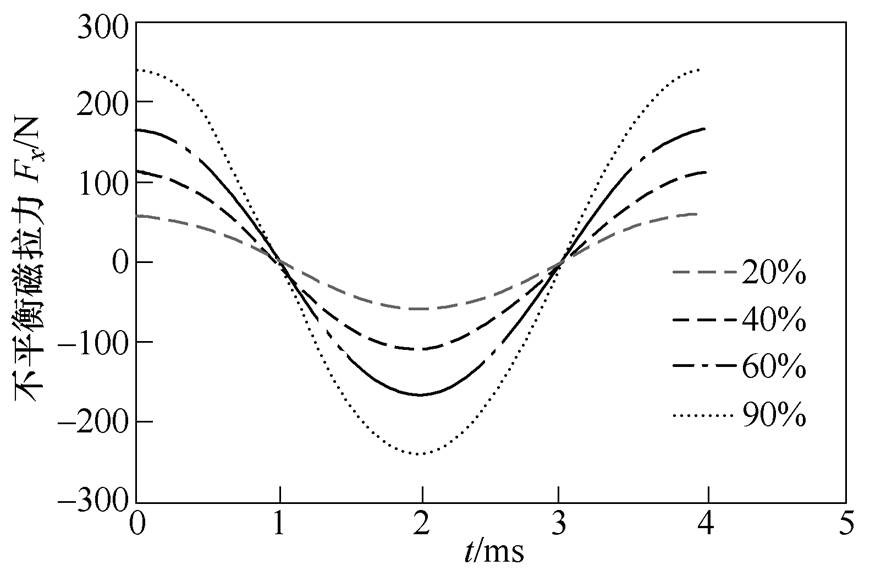
图11 动态偏心下x方向上的不平衡磁拉力
Fig.11 Unbalanced magnetic force of x direction with dynamic eccentricity
4 结论
本文首先建立了轴向磁通永磁电机气隙磁场解析计算模型,通过引入气隙磁导函数与端部效应函数计及开槽、端部效应对轴向磁通永磁电机气隙磁通密度的影响,在此基础上构建了气隙长度与偏心率之间的关系,计算了偏心状态下的气隙磁通密度,并对偏心状态下的受力进行了分析,得出如下结论:
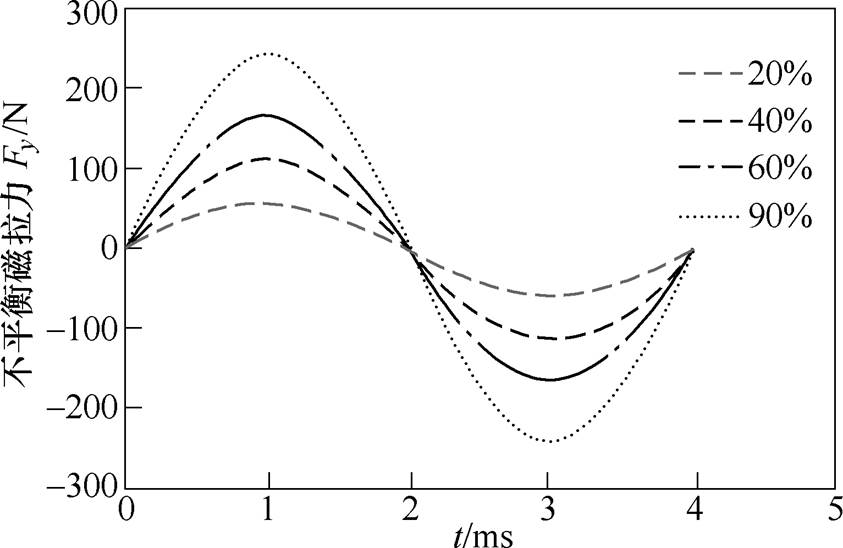
图12 动态偏心下y方向上的不平衡磁拉力
Fig.12 Unbalanced magnetic force of y direction with dynamic eccentricity
1)针对轴向磁通永磁电机三维有限元计算耗时的缺点,通过对气隙磁导函数、端部效应函数的傅里叶分解,在解析计算中引入其傅里叶函数,构建轴向磁通永磁电机气隙磁场解析计算模型,提高了轴向磁通永磁电机气隙磁通密度计算的速度与准确性。
2)偏心后的轴向磁通永磁电机,气隙磁场发生畸变,每对极下的磁场幅值均不等大小,动态偏心下的气隙磁场畸变高于静态偏心下的气隙磁场畸变。
3)偏心使轴向磁通永磁电机中产生不平衡磁拉力,随着偏心率的增加,不平衡磁拉力增大,静态偏心下,不平衡磁拉力不随时间变化,动态偏心下不平衡磁拉力随之间周期性变化。
参考文献
[1] 曹永娟, 黄允凯, 金龙. 磁极组合型轴向磁场无铁心永磁电机的设计与分析[J]. 中国电机工程学报, 2014, 34(6): 903-909.
Cao Yongjuan, Huang Yunkai, Jin Long. Design and analysis of a stator coreless axial-flux permanent magnet machine with module poles[J]. Proceedings of the CSEE, 2014, 34(6): 903-909.
[2] Huang Wanying, Bettayeb A, Kaczmarek R. Optimi- zation of magnet segmentation for reduction of eddy current losses in permanent magnet synchronous machine[J]. IEEE Transactions on Energy Con- version, 2010, 25(2): 381-387.
[3] Metin Aydin, Mehmet Gulec. A new coreless axial flux interior permanent magnet synchronous motor with sinusoidal rotor segments[J]. IEEE Transactions on Magnetics, 2016, 52(7): 125-130.
[4] 王晓远, 齐丹丹, 王辉. 定子无磁轭模块化轴向永磁电机磁极表面开槽分析[J]. 电工技术学报, 2017, 32(16): 145-152.
Wang Xiaoyuan, Qi Dandan, Wang Hui. Analysis on magnet surface groove of yokeless and segmented armature axial flux motor[J]. Transactions of China Electrotechnical Society, 2017, 32(16): 145-152.
[5] 左曙光, 吴双龙, 吴旭东, 等. 轴向磁通永磁同步电机转矩解析模型和转矩优化[J]. 电工技术学报, 2016, 31(23): 46-53.
Zou Shuguang, Wu Shuanglong, Wu Xudong, et al. Analytical model and optimization of torque of an axial flux permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2016, 31(23): 46-53.
[6] 鲍晓华, 吕强, 王汉丰. 基于齿部磁场分析的大型潜水电机气隙偏心故障研究[J]. 电工技术学报, 2016, 31(8): 90-95.
Bao Xiaohua, Lü Qiang, Wang Hanfeng. Study on air-gap eccentricity fault in large submersible motors with tooth magnetic field analysis[J]. Transactions of China Electrotechnical Society, 2016, 31(8): 90-95.
[7] Zhu Ziqiang, Wu Lijian, Mohd J M L. Influence of pole and slot number combinations on cogging torque in permanent-magnet machines with static and rotating eccentricities[J]. IEEE Transactions on Industry Applications, 2014, 50(5): 3265-3277.
[8] Kim U, Lieu D K. Magnetic field calculation in permanent magnet motors with rotor eccentricity: with slotting effect[J]. IEEE Transactions on Magnetics, 1998, 34(4): 2253-2266.
[9] Marignetti F, Vahedi A, Mirimani S M. An analytical approach to eccentricity in axial flux permanent magnet synchronous generators for wind turbines[J]. Electric Power Components and Systems, 2015, 43(9): 1039-1050.
[10] Araki S, Ind D, Kusatsu K, et al. Analyses of electromagnetic forces of concentrated winding permanent magnet brushless motors with rotor eccentricity[J]. Electrical Machines and Systems, 2009, 10(2): 1-4.
[11] Yu Yingquan, Bi Chao, Hla P N. Incline unbalanced magnetic pull induced by misalignment rotor in PMSM[J]. IEEE Transactions on Magnetics, 49(6): 2709-2714.
[12] Vansompel H, Sergeant P, Dupre L. A multilayer 2-D-2-D coupled model for eddy current calculation in the rotor of an axial-flux PM machine[J]. IEEE Transactions on Energy Conversion, 2012, 27(3): 784-791.
[13] Hendrik V, Peter S, Luc D. Effect of segmentation on eddy-current loss in permanent-magnets of axial-flux PM machines using a multilayer-2D: 2D coupled model[C]//Proceedings of the 20th International Conference on Electrical Machines, Marseille, France, 2012, DOI: 10.1109/ICElMach.2012.6349869.
[14] Mirimani S M, Vahedi A, Marignetti F. Effect of inclined static eccentricity fault in single stator-single rotor axial flux permanent magnet machines[J]. IEEE Transactions on Magnetics, 2012, 48(1): 143-149.
[15] 张冉, 王秀和, 杨玉波, 等. 基于等效剩磁法的永磁电动机转子偏心磁场解析计算[J]. 电工技术学报, 2009, 24(5): 7-13.
Zhang Ran, Wang Xiuhe, Yang Yubo, et al. Analytical prediction of magnetic field in permanent magnet motors with rotor eccentricity based on the method of equivalent remanence[J]. Transactions of China Electrotechnical Society, 2009, 24(5): 7-13.
Force Analyze of Axial Magnetic Flux Permanent Magnet Motor under Eccentricity Condition
Abstract In order to study the influence of eccentricity on the force of axial flux permanent magnet motor, an analytical model of the air gap magnetic field in the ideal state is established. The slot is also accounted for by introducing the air gap permeability function. The influence of the air gap magnetic field; through the analysis of the eccentric state of the axial flux permanent magnet motor, an analytical model of the air gap magnetic field in the eccentric state was established, and the accuracy of the analytical calculation model was verified by the finite element method. Based on the analytical method, calculation model of the unbalanced magnetic force of the axial flux permanent magnet motor under eccentric state is constructed, and the unbalanced magnetic force is calculated and analyzed. Regardless of static eccentricity or dynamic eccentricity, the amplitude of unbalanced magnetic force gradually increases with increasing eccentricity. Under static eccentricity, the unbalanced magnetic force does not change with time; under dynamic eccentricity, the unbalanced magnetic force changes periodically.
keywords:Axial magnetic flux permanent magnetic motor, air gap flux density, eccentricity, unbalanced magnetic force
中图分类号:TM315
DOI: 10.19595/j.cnki.1000-6753.tces.L80717
收稿日期2018-07-10
改稿日期 2019-08-31
张霄霆 男,1988年生,博士研究生,研究方向为特种电机及其控制。E-mail: 240535410@qq.com(通信作者)
张炳义 男,1954年生,教授,博士生导师,研究方向为电子-电气-机械一体化低速大转矩无齿轮传动系统的理论与技术。E-mail: 1392326904@qq.com
(编辑 崔文静)
文章来源:《电工技术学报》 网址: http://www.dgjszzs.cn/qikandaodu/2020/0521/341.html
上一篇:一种新型制动辅助系统的驱动方案
下一篇:电工类专业职业技能教学新思路 ——评《电工
电工技术学报投稿 | 电工技术学报编辑部| 电工技术学报版面费 | 电工技术学报论文发表 | 电工技术学报最新目录
Copyright © 2018 《电工技术学报》杂志社 版权所有
投稿电话: 投稿邮箱:

